Articolo riservato agli utenti registrati
Molte applicazioni hi-tech per smartphone e tablet utilizzano funzionalità rese possibili dall’integrazione di un accelerometro. Scopriamo come funziona questo componente e in che modo si utilizza.
Fino ad alcuni anni fa solo fisici e ingegneri avrebbero saputo dire cosa è un accelerometro, mentre oggi molti utenti di tablet e smartphone lo conoscono come quel sensore che permette di adattare la visualizzazione dello schermo (Fig. 1), ma anche come il sensore che nelle moderne console di gioco (per esempio Nintendo Wii) rileva il movimento del giocatore.
Usciti dal tradizionale campo di applicazione scientifico, soprattutto aerospaziale, gli accelerometri sono oggi utilizzati, oltre che nei dispositivi “mobile”, anche in campo automobilistico, nell’automazione, nell’analisi di sistemi meccanici e robotici. Tra le applicazioni che sfruttano gli accelerometri non può non essere menzionato il segway, un mezzo di trasporto che si mantiene in equilibrio su due ruote e il cui funzionamento è reso possibile dall’impiego di accelerometri, oltre che di giroscopi. Sistemi intelligenti di navigazione e di sicurezza montati sui mezzi di trasporto fanno inoltre sovente uso di accelerometri in combinazione con giroscopi e magnetometri.
Un accelerometro, come dice il nome stesso, è un dispositivo in grado di rilevare e misurare un’accelerazione cioè fisicamente una variazione di velocità nel tempo, anche se, come vedremo, ciò non comporta necessariamente che il dispositivo sia in movimento (si pensi all’accelerazione di gravità).
L’importanza assunta dagli accelerometri, soprattutto MEMS (la tecnologia con cui sono realizzati quelli per l’elettronica “mobile” e consumer) ci ha spinto a dedicare un articolo a tali componenti, dove spieghiamo il principio di funzionamento, ricorrendo a una descrizione analitica (modello matematico).

Fig. 1 Grazie all’accelerometro, lo smartphone capisce in che modo è orientato e adatta l’orientamento di immagini e schermate (Portrait e Landscape Mode).
Principio di funzionamento
Sebbene gli accelerometri MEMS siano, oltre che estremamente piccoli, anche tecnologicamente avanzati, come principio di funzionamento non differiscono molto da un accelerometro tradizionale di tipo meccanico. Tale dispositivo misura le accelerazioni dell’oggetto su cui è montato, anzi, per l’esattezza, rileva una forza, ma siccome, in base alla Seconda legge della dinamica di Newton le due cose sono legate dalla massa dell’oggetto utilizzato a riferimento (che resta costante), il discorso è ugualmente valido.
Capite ciò considerando che un accelerometro tradizionale meccanico contiene una massa (caratterizzata da un peso, il quale è pari alla massa moltiplicata per l’accelerazione di gravità, pari a circa 9.81 m/s²) collegata a una molla che presenta l’altra estremità fissata alla parete interna di un involucro. Detta massa in Fig. 2 è rappresentata da una sfera.
Se l’involucro viene sottoposto a una forza o a un’accelerazione, anche la massa al suo interno si muove allungando o comprimendo la molla. Supponendo che la molla sia orientata nella direzione del movimento (verticale per esempio), misurando la compressione o l’allungamento della molla è possibile determinare l’accelerazione dell’involucro.
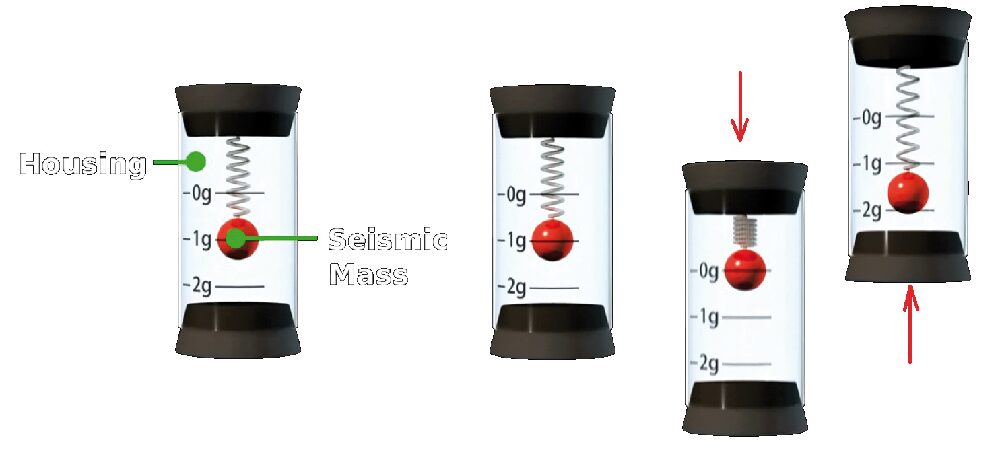
Fig. 2 Un accelerometro meccanico può essere immaginato come un involucro dove una molla fissata ad esso da un’estremità, è applicata a una massa.
Se si usano tre accelerometri orientati lungo le tre direzioni spaziali, x, y e z, si possono anche misurare le componenti dell’accelerazione dell’oggetto nello spazio (Fig. 3).
Il principio di funzionamento di un accelerometro è quindi basato sull’inerzia di una massa sottoposta ad un’accelerazione. La massa si sposta rispetto all’involucro, in direzione opposta all’accelerazione, di una quantità proporzionale all’accelerazione stessa e alla massa, e inversamente proporzionale alla costante elastica della molla.
Un accelerometro elettronico sfrutta lo stesso principio e in più trasforma lo spostamento in un segnale elettrico che può essere acquisito e utilizzato da una MCU.
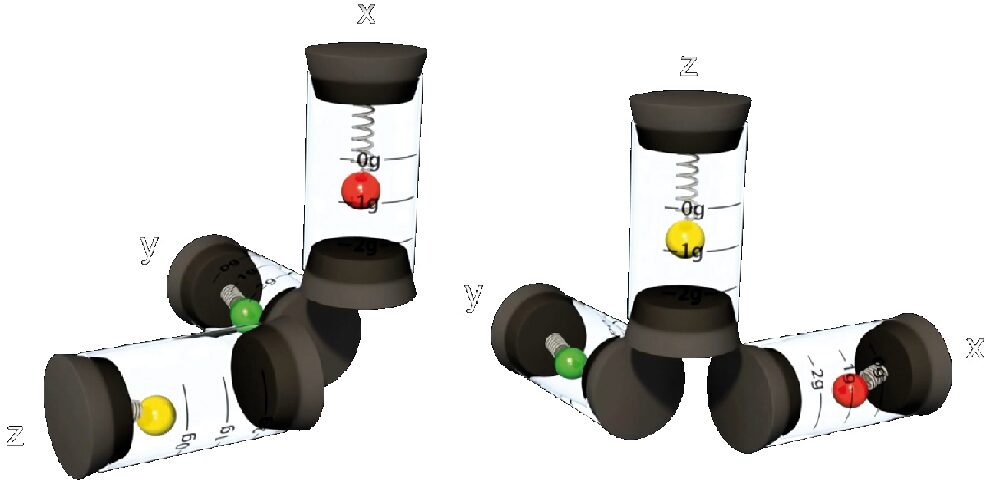
Fig. 3 Utilizzando tre accelerometri orientati lungo le tre direzioni spaziali x, y e z si ottiene un sistema in grado di misurare le componenti dell’accelerazione nello spazio.
La schematizzazione di Fig. 2 può essere resa più reale modificandola come in Fig. 4, dove la sfera è posizionata al centro di un cubo ed è ivi sospesa attraverso tre coppie di molle agganciate, ciascuna, da una estremità alla sfera e dall’altra al centro della rispettiva faccia del cubo.
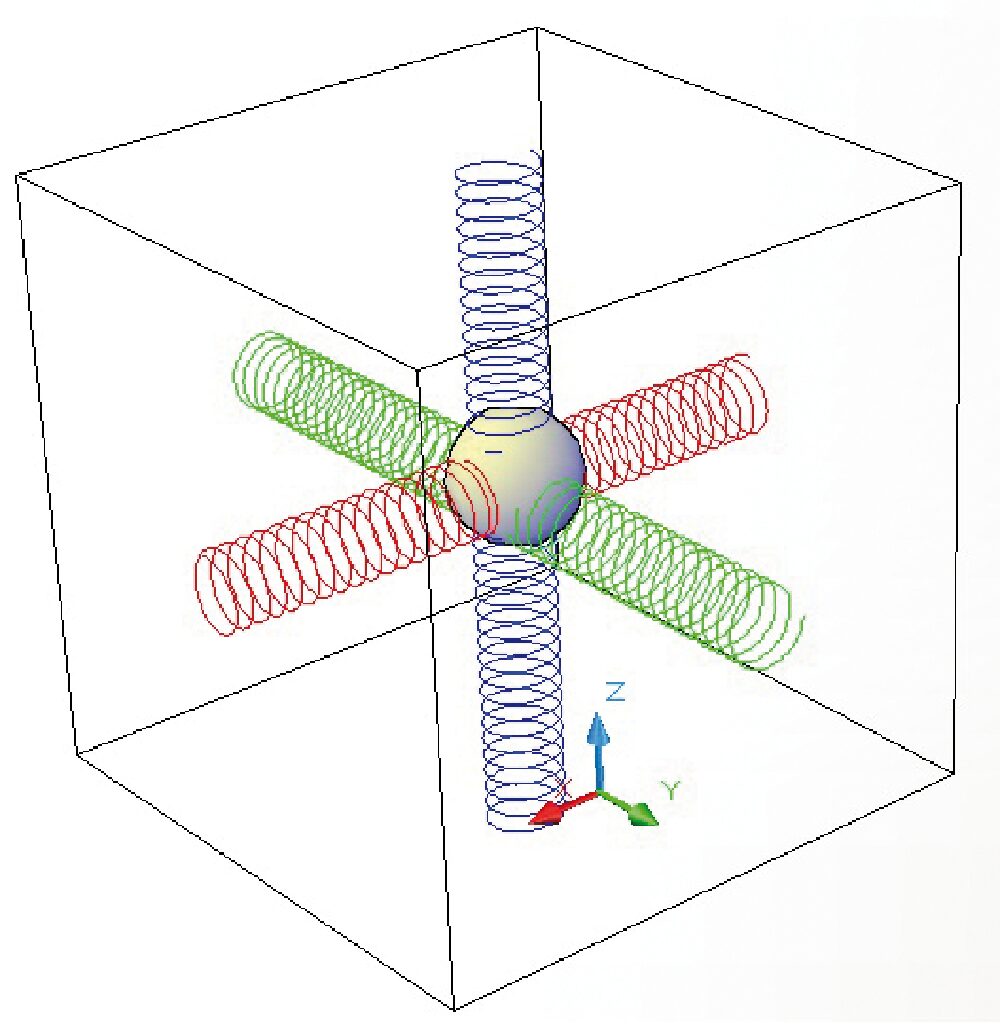
Fig. 4 Modello meccanico di un accelerometro a tre assi.
Muovendo il cubo nello spazio, la sfera si sposta rispetto all’involucro, dalla sua posizione di equilibrio iniziale; a tale movimento si oppongono le molle, che si allungano e comprimono mantenendola sospesa. Ciascuna coppia di molle è ortogonale alle altre due e si trova disposta nella direzione di uno degli assi cartesiani.
A causa della forza di gravità, l’effetto reale che si osserva, in condizioni di riposo, non è quello di Fig. 4, ma quello di Fig. 5 (nell’ipotesi che la gravità agisca in direzione perpendicolare al piano xy).
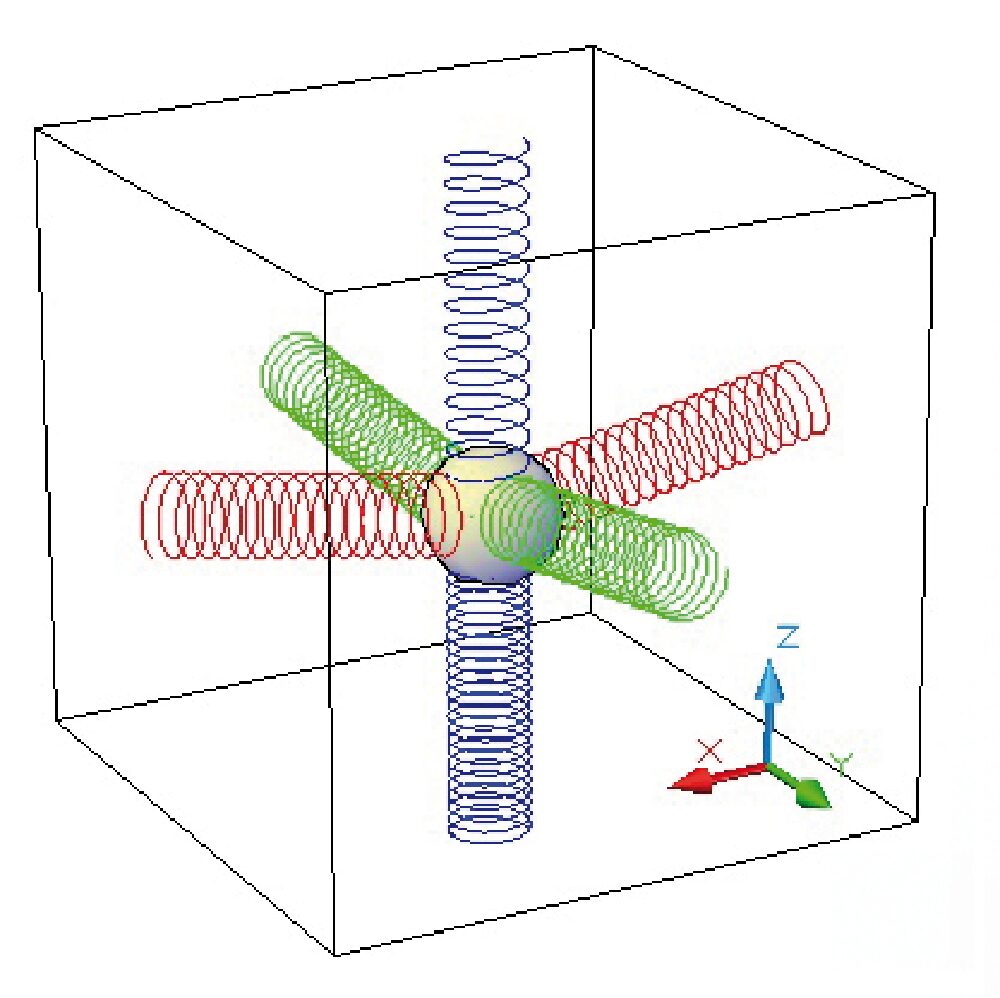
Fig. 5 Modello meccanico di un accelerometro a tre assi.in condizioni di riposo soggetto alla gravità (diretta lungo z).
Tipologie di accelerometri
Esistono accelerometri a un solo asse, a due o a tre assi; considerate che con uno a tre assi è possibile fare tutto quello che si può fare anche con un accelerometro a uno o due assi ma a costo ovviamente maggiore. Tipologia (principio di conversione da grandezza fisica a grandezza elettrica), caratteristiche tecniche, sensibilità e costo determinano il campo applicativo di un accelerometro. In generale, gli accelerometri possono essere divisi in due categorie:
– per misure di accelerazioni statiche;
– per misure di accelerazioni dinamiche.
Gli accelerometri per misure di accelerazione dinamica non sono in grado di rilevare accelerazioni statiche (come quella di gravità)essendo fatti per rilevare accelerazioni che variano nel tempo come quelle generate dalle vibrazioni o negli urti.
Accelerometri di questo tipo sono quelli piezoelettrici. Esistono anche accelerometri in grado di rilevare entrambi i tipi di accelerazione. Tra le caratteristiche da tenere in considerazione nella scelta di un accelerometro c’è anche la banda passante, che deve essere commisurata alla rapidità con cui evolve il fenomeno da rilevare.
La miniaturizzazione dell’elettronica consente oggi l’integrazione, nel package del sensore, anche dei circuiti che servono a condizionare il segnale; grazie ad essi, non solo il sensore riceve la corretta alimentazione, ma è anche in grado di amplificare e filtrare adeguatamente il segnale e in alcuni casi di eseguire operazioni più complesse come la linearizzazione della propria caratteristica di trasferimento.
Di seguito descriviamo le principali tipologie di accelerometri distinte in base al principio di conversione dell’accelerazione in segnale elettrico.
Accelerometro estensimetrico
Si tratta di un accelerometro a ponte che sfrutta come principio la variazione di resistenza di un estensimetro provocata da una variazione di lunghezza generata a sua volta da un’accelerazione. In esso una massa viene sospesa su dei sottili lamierini sui quali sono fissati degli estensimetri collegati a ponte di Wheatstone.
In presenza di un’accelerazione, la massa si sposta, i lamierini si flettono e gli estensimetri subiscono un allungamento che genera una variazione di resistenza. La tensione di sbilanciamento del ponte Wheatstone che ne consegue, risulta in tal modo proporzionale all’accelerazione e la sua misura consente di risalire al valore di accelerazione. Una variante dell’accelerometro estensimetrico è quello piezoresistivo, che differisce perché impiega sensori piezoresistivi al posto di quelli estensimetrici.
Accelerometro LVDT
Acronimo di Linear Variable Differential Transformer, questo accelerometro sfrutta ancora lo spostamento di una massa ma ne rileva l’entità secondo un principio differente; la massa, realizzata in materiale ferromagnetico, è sospesa su molle o elementi elastici all’interno di un canale attorno al quale sono avvolte delle bobine.
L’effetto induttivo dovuto al movimento della massa, che fa da nucleo, può essere misurato elettricamente. Da esso è possibile risalire all’andamento della posizione del nucleo rispetto alle bobine e quindi all’accelerazione cui la massa è soggetta.
Accelerometro capacitivo
Rileva lo spostamento della massa misurando la variazione della capacità di un condensatore, la cui distanza tra le armature varia a seguito dell’accelerazione. In pratica, la massa mobile è contrastata da un elemento elastico antagonista (tipicamente una membrana) e costituisce un’armatura del condensatore, mentre l’altra armatura è fissa.
La variazione di capacità risulta pertanto proporzionale allo spostamento dell’armatura mobile e quindi all’accelerazione cui il sensore è sottoposto. Un circuito capacimetro in grado di generare un segnale elettrico proporzionale alla variazione di capacità consente la misura dell’accelerazione.
Accelerometro piezoelettrico
Sfrutta la tensione che un cristallo piezoelettrico genera quando è sottoposto a compressione. La massa viene sospesa sul cristallo piezoelettrico che fa quindi sia da sensore che da elemento elastico. In presenza di accelerazione, la massa modifica la pressione esercitata sul cristallo, che genera un segnale elettrico proporzionale. Si tratta di accelerometri spesso poco sensibili.
Questo aspetto, sebbene in alcune applicazioni risulti indesiderato, in altre può risultare vantaggioso, specie quando è necessario rilevare accelerazioni elevatissime (anche centinaia di g). Sebbene il cristallo generi un segnale elettrico proporzionale alla compressione, se questa permane, il segnale tende a scomparire, quindi un accelerometro del genere non è adatto a rilevare accelerazioni statiche ma solo accelerazioni dinamiche.
Accelerometro laser
È un sensore utilizzato quando serve effettuare misure estremamente precise; misura istante per istante lo spostamento dell’oggetto e un controllore o una MCU acquisisce questa informazione e calcola l’accelerazione dell’oggetto come derivata seconda della posizione rispetto al tempo. Ha il vantaggio di poter essere utilizzato anche non montato sull’oggetto in movimento.
Accelerometri MEMS
Bene, dedichiamoci ora agli accelerometri più utilizzati. La tecnologia MEMS non riguarda solo i moderni accelerometri ma anche altri tipi di sensori. Un minuscolo chip di silicio diventa ora un sensore di pressione, ora un accelerometro, ora un giroscopio e così via, integrando spesso non solo le funzioni di rilevazione ma anche quelle di elaborazione e attuazione.
La sigla MEMS sta per Micro Electro-Mechanical Systems e identifica sensori la cui dimensione media è dell’ordine del micron e che integrano parti il cui comportamento coinvolge sia la meccanica che l’elettronica, sullo stesso substrato di silicio, coniugando le proprietà elettriche dei semiconduttori con quelle opto-meccaniche. Le applicazioni di questa tecnologia si sono rapidamente diffuse sconfinando ben presto nel mercato delle applicazioni consumer. La tecnologia è in continua evoluzione, tanto che già si parla di Nano Electro-Mechanical System o NEMS.
L’accelerometro, sebbene sia su chip di silicio, è ancora costituito da una massa, stavolta composta da lamelle mobili e fisse tra loro intercalate; l’accelerazione le fa deformare determinando una variazione della distanza tra esse e quindi della capacità (Fig. 6 e Fig. 7). In Fig. 8 è riportata la struttura di un accelerometro MEMS visto al microscopio elettronico, che conferma la struttura schematizzata in Fig. 6. La struttura superiore (upper proof mass) si comporta meccanicamente come una molla; la forza di gravità o un’accelerazione esterna del package ne causano la deformazione. La struttura è elettricamente assimilabile a un condensatore a tre armature, come schematizzato in Fig. 7. Il circuito interno converte la variazione di capacità in un segnale elettrico analogico o digitale.
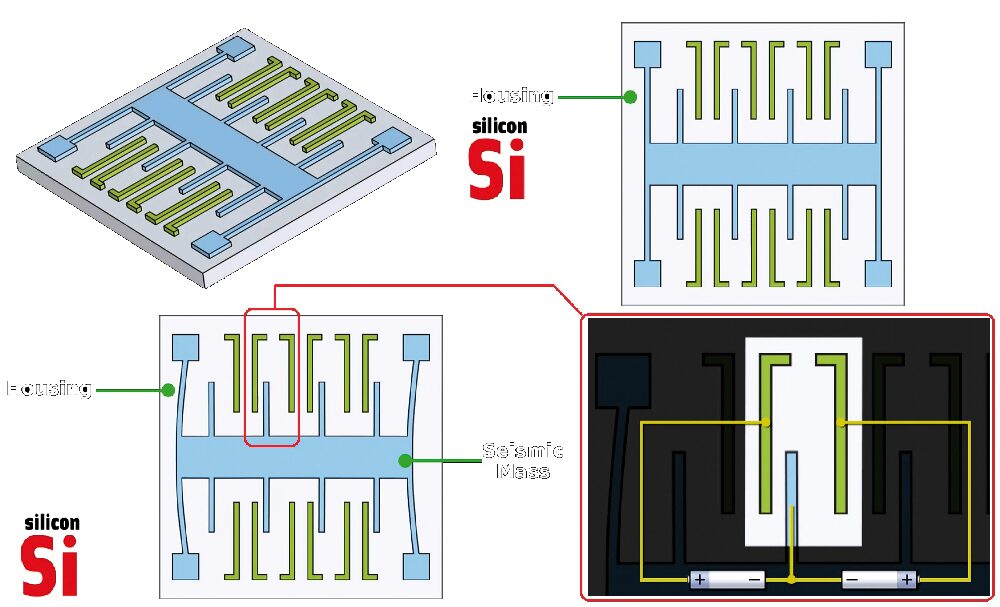
Fig. 6 Nell’accelerometro MEMS c’è una massa composta da lamine mobili intercalate a lamine fisse; la deflessione di quelle mobili provoca una variazione di capacità consentendo la trasduzione dell’accelerazione in segnale elettrico.
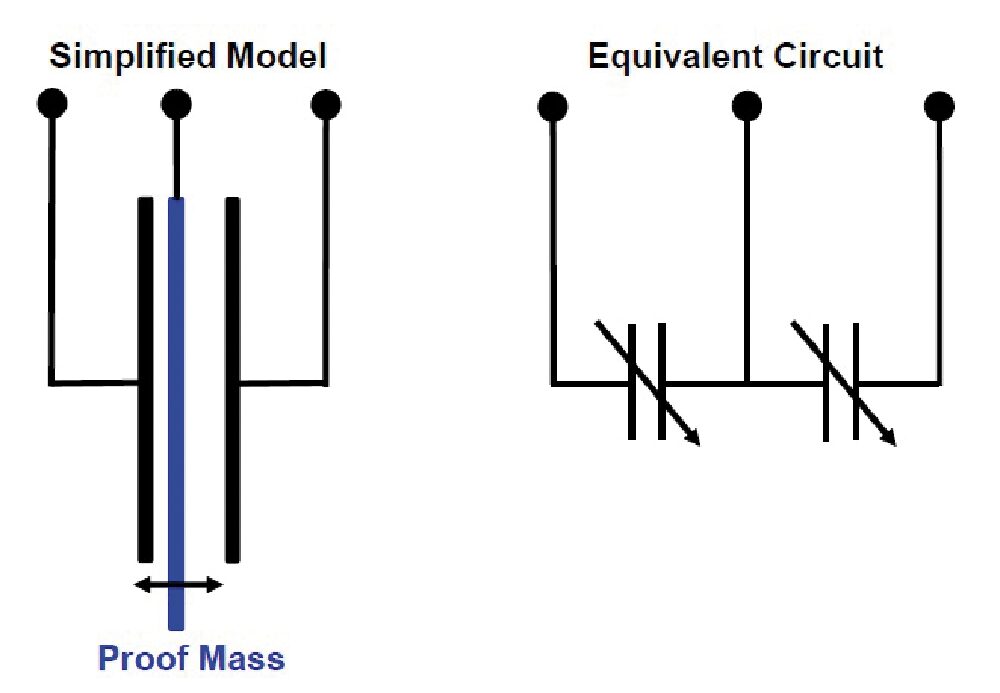
Fig. 7 Modello equivalente elettrico di un accelerometro MEMS.
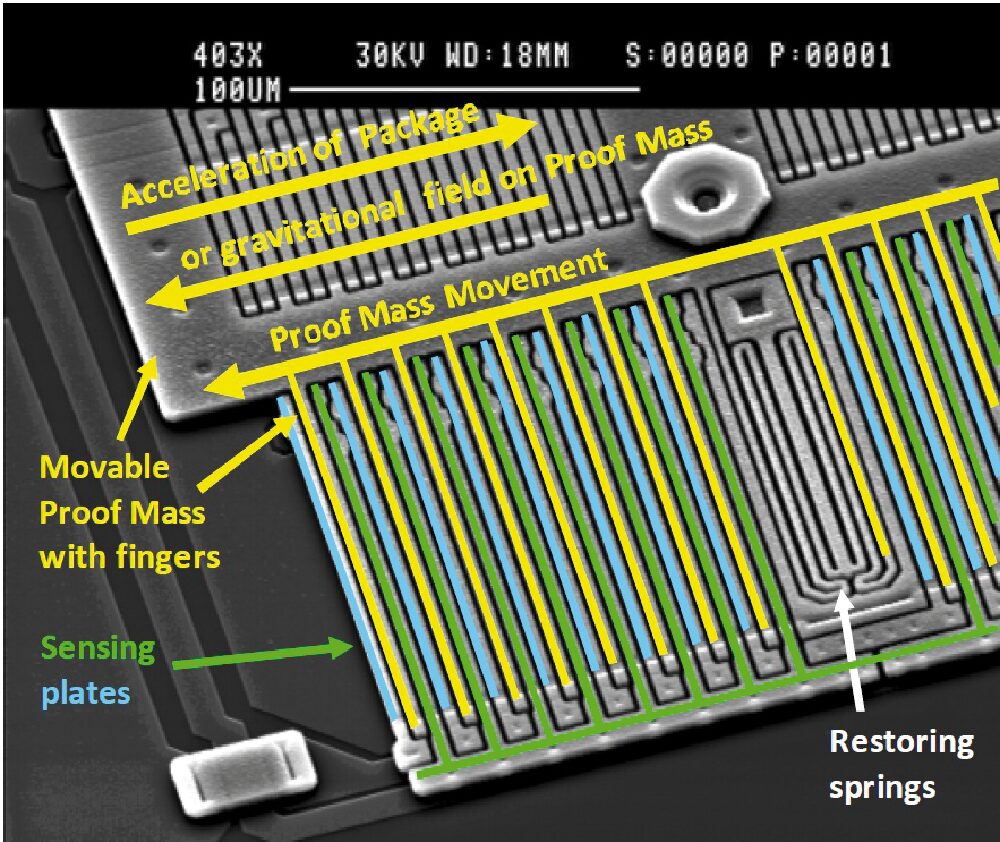
Fig. 8 Immagine ripresa al microscopio elettronico di un accelerometro MEMS. Si notano la massa fissa e la massa mobile.
L’accelerometro come inclinometro
Un modo per determinare l’inclinazione (tilt sensing) di un oggetto consiste nell’integrare l’uscita di un giroscopio. Grazie alla capacità di sentire un’accelerazione (e quindi anche l’accelerazione di gravità), anche un accelerometro può essere utilizzato per misurare l’inclinazione. In un’applicazione di tilt sensing si considera l’accelerazione di gravità come l’unica agente sul dispositivo. Questo significa, tra le altre cose, ignorare accelerazioni superiori a 1g (dove con g indichiamo, come è convenzione, l’accelerazione di gravità) oltre alla possibilità di utilizzare sensori con campo di misura relativamente contenuto.
Con riferimento allo schema di principio di Fig. 5, in presenza della sola gravità, la direzione le cui molle si allungano soltanto ma non si comprimono, è quella lungo la quale non vi è accelerazione. Tali direzioni possono essere evidentemente una o due, ma mai tre (condizione assurda geometricamente) e nemmeno zero, poiché significherebbe assenza di gravità (ammesso che l’accelerometro sia fermo e non in caduta libera).
Dall’allungamento e compressione delle molle, con un po’ di trigonometria è possibile capire come l’oggetto è inclinato. Da un punto di vista fisico il tutto è esatto a patto che l’oggetto non sia sottoposto ad altre accelerazioni ad eccezione di quella di gravità. Per non incorrere in errori di terminologia è opportuno definire, a questo punto, cosa si intenda con i termini angolo di Roll, Pitch e Yaw che significano rispettivamente rollìo, beccheggio e imbardata e che sono presi in prestito dal volo.
Se consideriamo x l’asse diretto dalla coda alla testa di un velivolo, y quello diretto dall’ala sinistra a quella destra e z quello diretto perpendicolarmente ai primi due a formare una terna destrogira (diretto quindi come la gravità, se il velivolo è in assetto orizzontale) allora una rotazione del velivolo intorno ad x prende il nome di rollio (Roll), intorno a y di beccheggio (Pitch) e intorno a z di imbardata (Yaw).
Dunque, se gli assi x e y dell’accelerometro si trovano sul piano dell’orizzonte e z è quindi perpendicolare a esso, l’accelerometro è in grado di rilevare, a partire da questa posizione, un rollio o un beccheggio, ma non un’imbardata, perché la rotazione intorno a z non provoca alcuna variazione nella scomposizione dell’accelerazione di gravità lungo i tre assi. In pratica per rilevare anche l’angolo di imbardata sarebbe necessario aggiungere al sistema un giroscopio.
La Fig. 9 è esplicativa a riguardo, poiché mostra le uscite analogiche dell’accelerometro in diverse posizioni (assetti rispetto all’accelerazione di gravità).
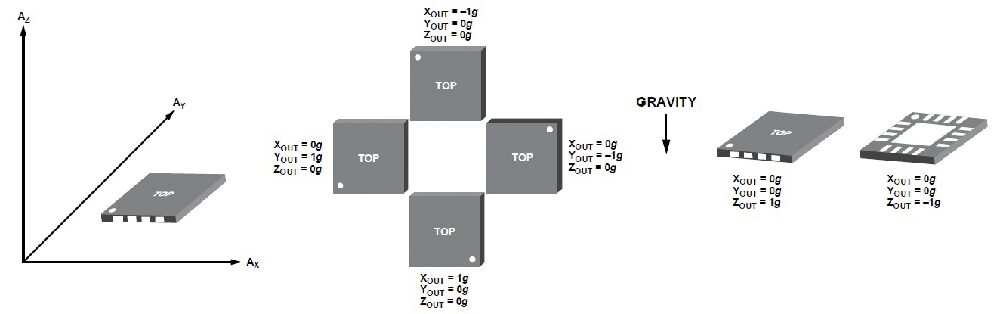
Fig. 9 Uscite analogiche dell’accelerometro in diverse assetti rispetto all’accelerazione di gravità.
Nella condizione in cui solo la componente z è non nulla, possiamo dire che l’oggetto ha assunto posizione orizzontale ma non è possibile affermare di quale degli infiniti assetti orizzontali si tratti. Analogamente, quando l’asse y diventa parallelo all’accelerazione di gravità, qualunque rotazione intorno ad y genera sempre la stessa uscita (Xout=o, Yout=±g, Zout=0) e qualcosa di analogo può dirsi quando l’accelerometro ruota intorno ad un asse generico purché parallelo all’accelerazione di gravità. Queste osservazioni consentono di capire perché l’affermazione secondo la quale un accelerometro a tre assi consente di determinare l’orientamento dell’oggetto nello spazio non è del tutto corretta.
L’assunzione principale è che l’unica accelerazione cui l’accelerometro è soggetto è quella di gravità; nella pratica, anche se il segnale proveniente dall’accelerometro non é dovuto esclusivamente alla gravità, se ne possono filtrare, per esempio, componenti ad alta frequenza che sicuramente non sono dovute alla gravità.
La forza di gravità è in ogni caso una forza statica cui corrisponde pertanto un’accelerazione statica e qualunque altra accelerazione vi si sovrapponga tende a falsare la misura: pensate ad esempio a un’accelerazione costante diversa dalla gravità, come quella che si ha a bordo di un veicolo che aumenta o diminuisce gradualmente la sua velocità con un tasso di variazione costante nel tempo lungo un percorso rettilineo, oppure a quella che si verifica a bordo di un veicolo che percorre a velocità angolare costante una curva (cosa che comporta un’accelerazione centripeta costante).
Per comprendere meglio il tutto descriviamo matematicamente il funzionamento dell’inclinometro.
Con riferimento ad un sistema a un solo asse (Fig. 10), ruotiamo di un angolo θ l’accelerometro disposto lungo l’asse x solidale con esso e inizialmente orientato lungo l’orizzontale.
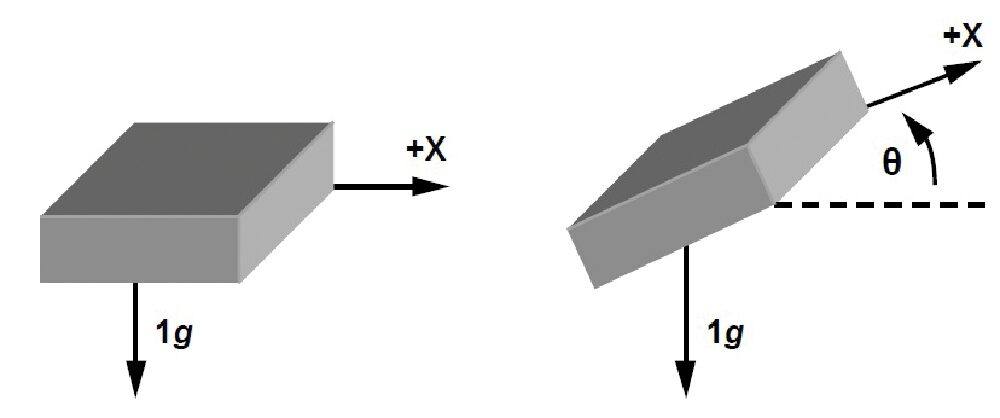
Fig. 10 Accelerometro ruotato di un angolo θ rispetto al piano orizzontale.
La proiezione del vettore di gravità g sull’asse x è pari a:
AX,OUT [g] = 1 g sin(θ) [1]
Questa relazione trigonometrica mostra una sensibilità nella misura dell’angolo di inclinazione inferiore per angoli prossimi a zero e per angoli vicini a 90 gradi (Fig. 11).
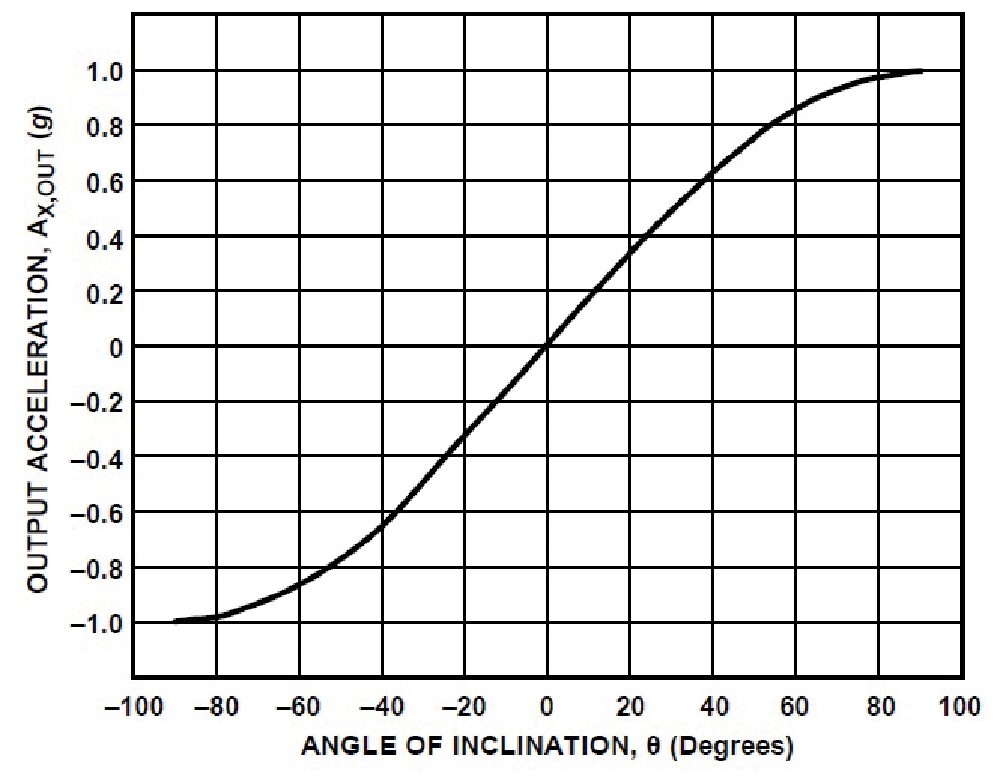
Fig. 11 Tipico andamento dell’uscita di un accelerometro analogico a un solo asse in funzione dell’angolo di inclinazione.
L’angolo di inclinazione in radianti può essere espresso dall relazione:
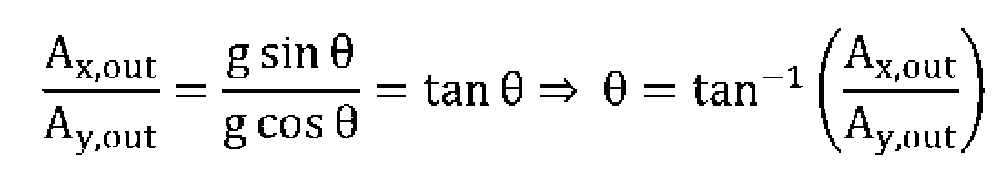
Una limitazione della misura su un solo asse è che non è possibile rilevare l’angolo di inclinazione in tutto il range di variazione pari a 360° dal momento che la componente lungo x dell’accelerazione, in presenza di un’inclinazione N°, è la stessa che si ottiene per una inclinazione pari a 180° − N°. Se si vuole distinguere l’inclinazione sugli interi 360° è necessario disporre di un accelerometro a due assi o di due accelerometri a un asse (Fig. 12).
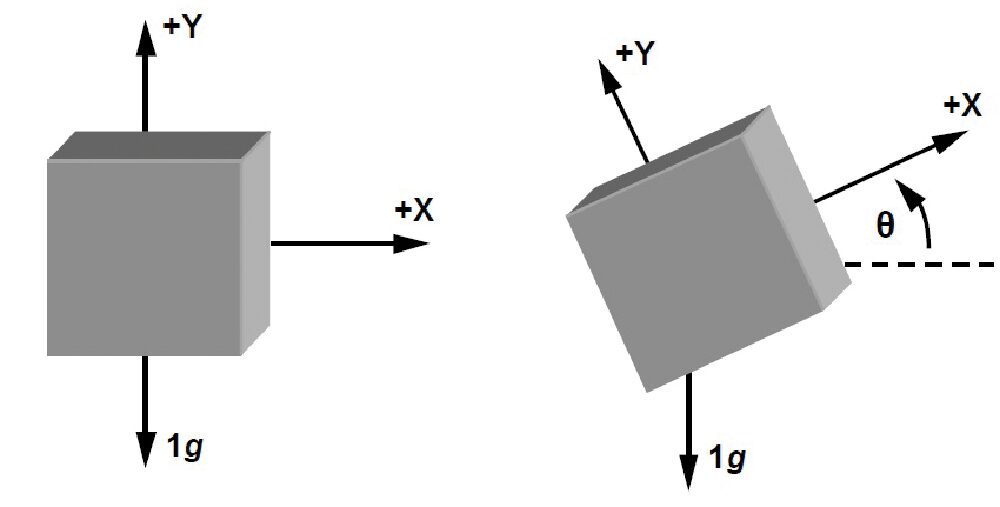
Fig. 12 Tilt sensing per un accelerometro a due assi.
La componente dell’accelerazione valutata lungo l’asse x è proporzionale al seno dell’angolo di inclinazione, quella lungo l’asse y è proporzionale al coseno. Quando la sensibilità della misura si riduce lungo un asse, aumenta lungo l’altro (Fig. 13).
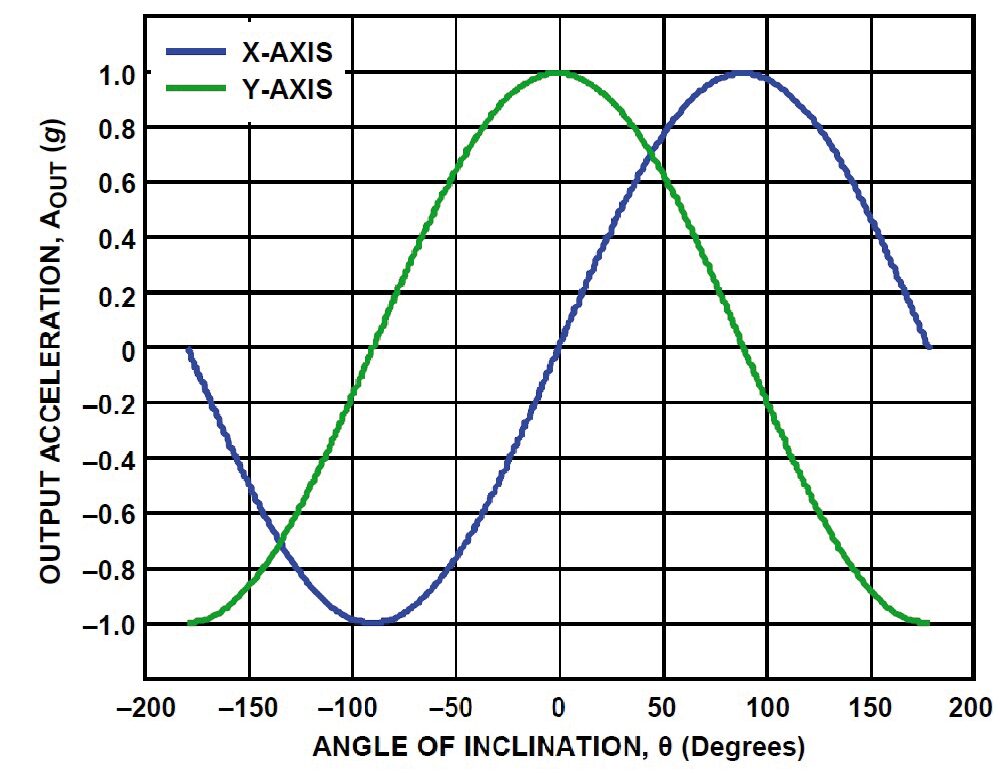
Fig. 13 Uscite (componenti) di un accelerometro a due assi in funzione dell’angolo di inclinazione.
La possibilità di misurare le due componenti consente di definire l’angolo di inclinazione come:
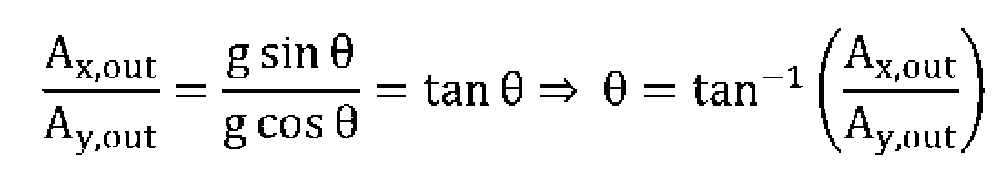
La funzione arcotangente restituisce un angolo del primo o del terzo quadrante se il rapporto AX,OUT/AY,OUT è positivo e del quarto o secondo quadrante se il rapporto risulta negativo. Per la corretta determinazione del quadrante si esamina il segno delle componenti dell’accelerazione dal momento che in nessun quadrante abbiamo seno e coseno uguali in valore e segno a quelli di un angolo di un altro quadrante (Fig. 14).
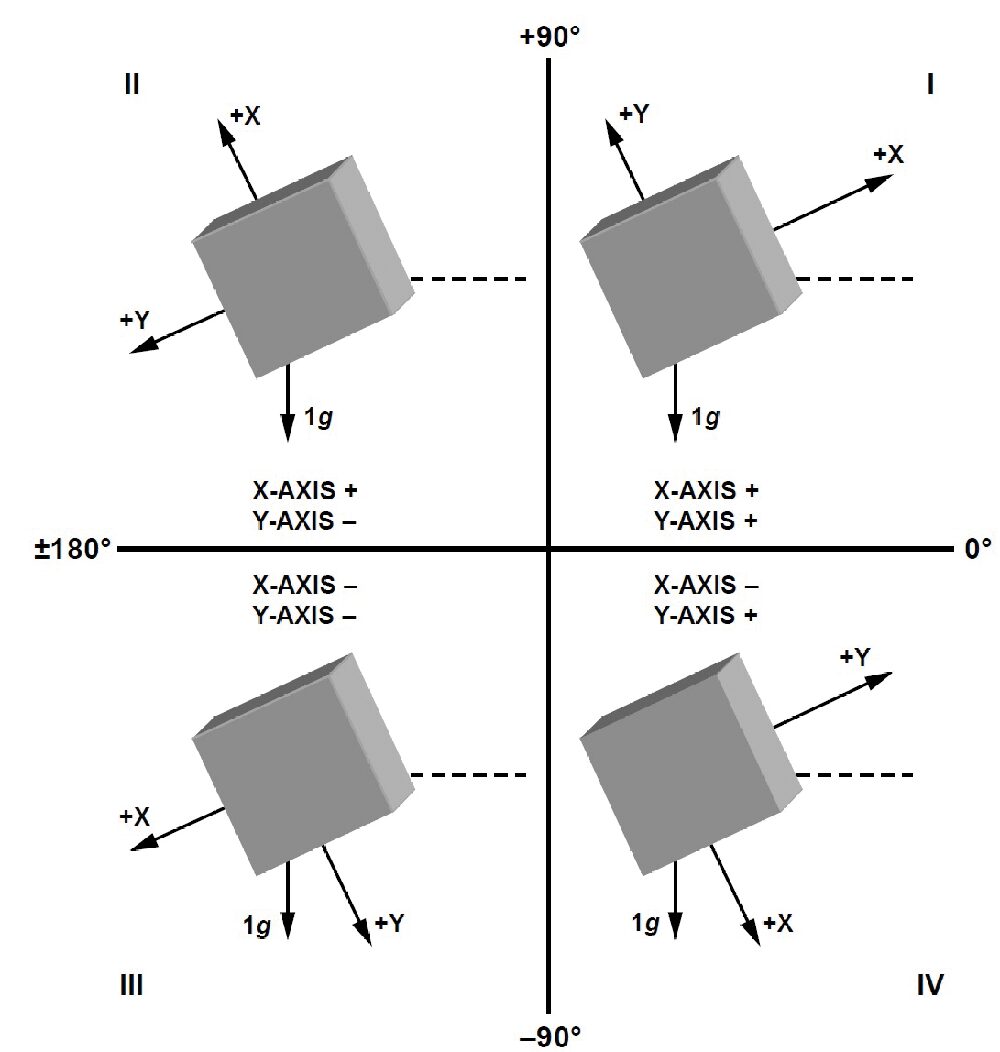
Fig. 14 Con un accelerometro a due assi è possibile misurare l’inclinazione commettendo un errore più contenuto ed è possibile distinguere tra i diversi quadranti dal momento che in nessun quadrante abbiamo seno e coseno uguali, come valore e segno, a quelli di un angolo di un altro quadrante.
I
n un sistema a tre assi (Fig. 15) è possibile determinare l’orientamento di ciascuno degli assi dell’accelerometro rispetto a una posizione di riferimento in cui tipicamente gli assi x ed y coincidono con il piano orizzontale (perpendicolare a g) e l’asse z è perpendicolare a questo piano (quindi coincidente con la gravità). θ è l’angolo tra il piano orizzontale e l’asse x dell’accelerometro, ψ quello tra il piano orizzontale e l’asse y dell’accelerometro e φ quello tra la gravità e l’asse z.
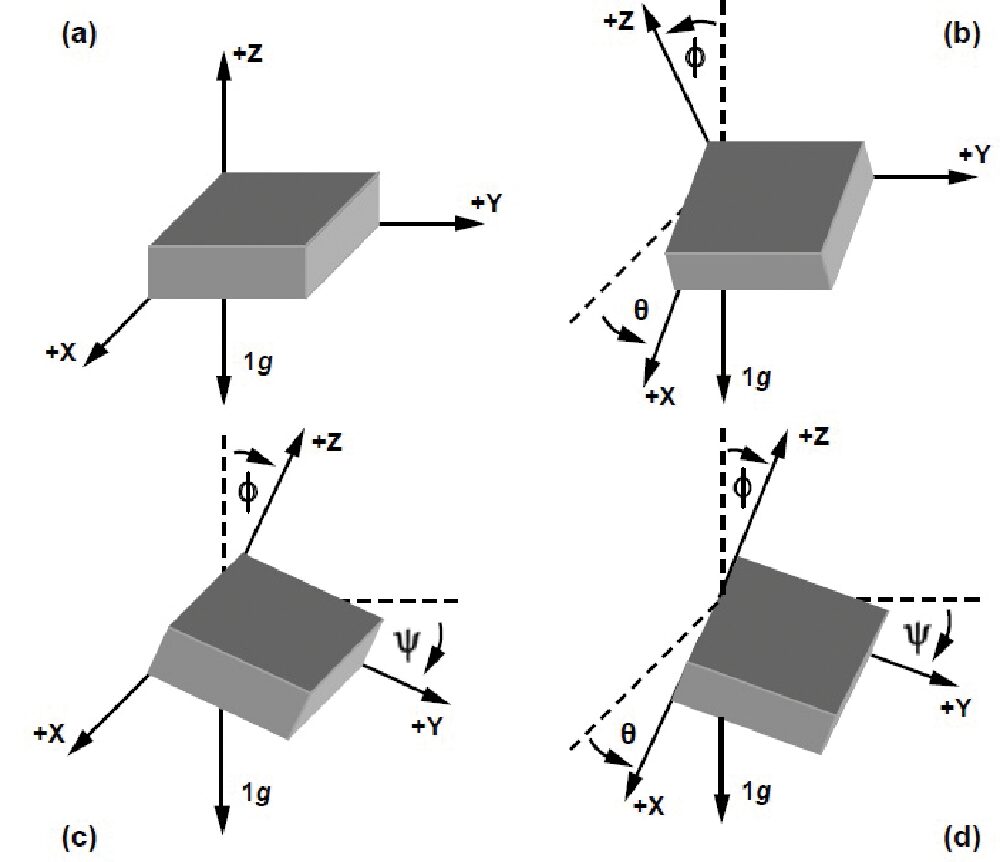
Fig. 15 Con un accelerometro a tre assi è possibile determinare l’orientamento di ciascuno degli assi dell’accelerometro rispetto a una posizione di riferimento.
Considerando come posizione iniziale quella in cui g coincide con l’asse z tutti gli angoli sono nulli, i tre angoli risultano espressi dalle seguenti relazioni:
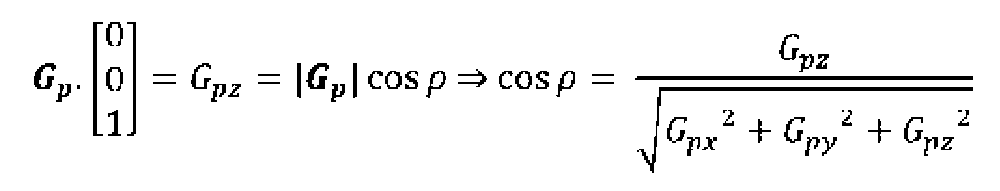
Se l’accelerometro è fermo nella posizione iniziale solo Az è non nulla e i tre angoli risultano nulli come ci aspettiamo.
Qualche considerazione
Gli accelerometri in commercio si suddividono in analogici e digitali. I primi sono caratterizzati da tante uscite analogiche quanti sono gli assi di misura. Ciascuna uscita è rappresentata elettricamente da una tensione proporzionale al valore della componente dell’accelerazione lungo quell’asse espressa come fattore di g. Se per esempio si impiega un accelerometro analogico funzionante tra 0V e 2V, in grado di misurare al massimo 1g, allora abbiamo sugli assi uscita 1V quando l’accelerazione vale 0g, 2V se vale 1g e 0V se vale -1g. Interfacciando a un accelerometro analogico una MCU che integri dei convertitori A/D è possibile digitalizzare ed elaborare la misura.
Spesso si presenta la necessità di condizionare il segnale analogico a causa del rumore che si sovrappone al segnale stesso e che si manifesta come una continua oscillazione dei valori analogici prodotti, anche se l’accelerometro è fermo (questo effetto può essere ridotto utilizzando opportuni filtri passa-basso).
Gli accelerometri digitali aggiungono semplicemente alla parte analogica la digitalizzazione del segnale e presentano tipicamente una linea di comunicazione con la MCU di tipo I²C o SPI. Un accelerometro che funzioni in maniera appropriata deve inoltre essere caratterizzato da un offset il più contenuto possibile, idealmente zero e da una sensibilità sufficientemente elevata, commisurata alla specifica applicazione.
Limitandoci alla questione dell’offset e riferendoci a un accelerometro a due assi, se consideriamo un offset di 50 mg lungo l’asse x (dove g è l’accelerazione di gravità), a 0° l’asse x legge 50 mg anche se dovrebbe leggere 0 mentre l’asse y legge 1 g da cui consegue un errore di 2,9°. L’errore varia in funzione dell’orientamento come rappresentato in Fig. 16. Queste poche considerazioni servono a darci un’idea del legame che esiste tra le caratteristiche di un accelerometro e gli errori più elementari insiti nella misura.
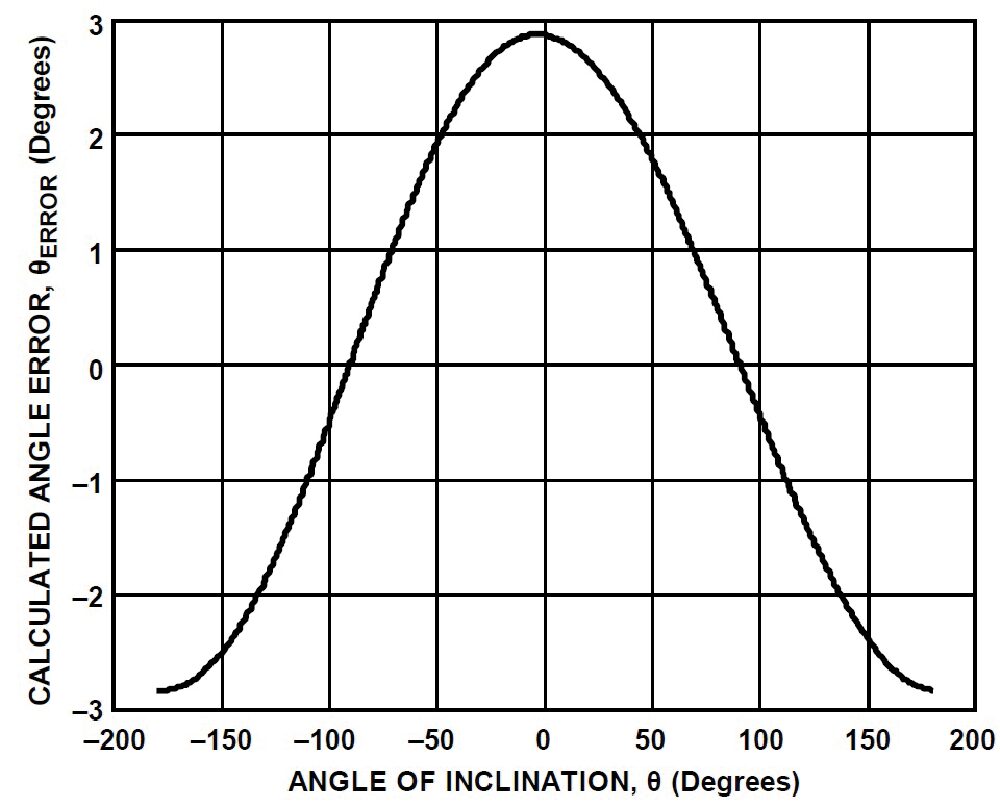
Fig. 16 L’offset di misura ha un peso sull’errore che è funzione dell’angolo di inclinazione da misurare.
Modello matematico basato sulle matrici di rotazione
Vogliamo ora mostrare come può essere descritto il funzionamento di un accelerometro a tre assi con l’ausilio delle matrici di rotazione. Prima di procedere, occorre sottolineare alcuni concetti:
1. un accelerometro a tre assi è caratterizzato da una terna di assi solidali con se stesso; se è soggetto a un’accelerazione diretta lungo uno solo di questi assi solo quella uscita risulterà diversa da zero, diversamente saranno diverse da zero tutte le uscite lungo i quali assi il vettore accelerazione presenta componente non nulla;
2. fino a questo momento abbiamo considerato l’accelerazione di gravità come l’unica agente sull’accelerometro; in generale, un accelerometro misura la differenza tra l’accelerazione lineare e l’accelerazione di gravità, di conseguenza, in assenza di accelerazione lineare (oggetto fermo o in movimento a velocità costante in una direzione fissa) l’accelerometro è in grado di misurare le componenti dell’accelerazione g lungo i suoi tre assi;
3. un oggetto può essere portato in un determinato assetto nello spazio seguendo tre rotazioni che secondo il linguaggio aeronautico sono le rotazioni di rollio (roll), beccheggio (pitch) e imbardata (yaw), da eseguire convenzionalmente secondo questa sequenza poiché l’assetto finale dipende non solo dal valore delle singole rotazioni ma anche dall’ordine con cui esse si susseguono;
4. un movimento intorno a un solo asse coincidente con il vettore gravità non può essere rilevato da un accelerometro perché le tre componenti del vettore g rimangono invariate.
Prendendo ad esempio uno smartphone, nel prosieguo utilizzeremo il sistema di riferimento destrogiro solidale con l’apparecchio (e con l’accelerometro in esso integrato) riportato in Fig. 17. L’asse z è pertanto orientato verso il basso, cioè lungo il vettore g quando si poggia l’apparecchio sul piano di un tavolo con lo schermo rivolto verso di noi.
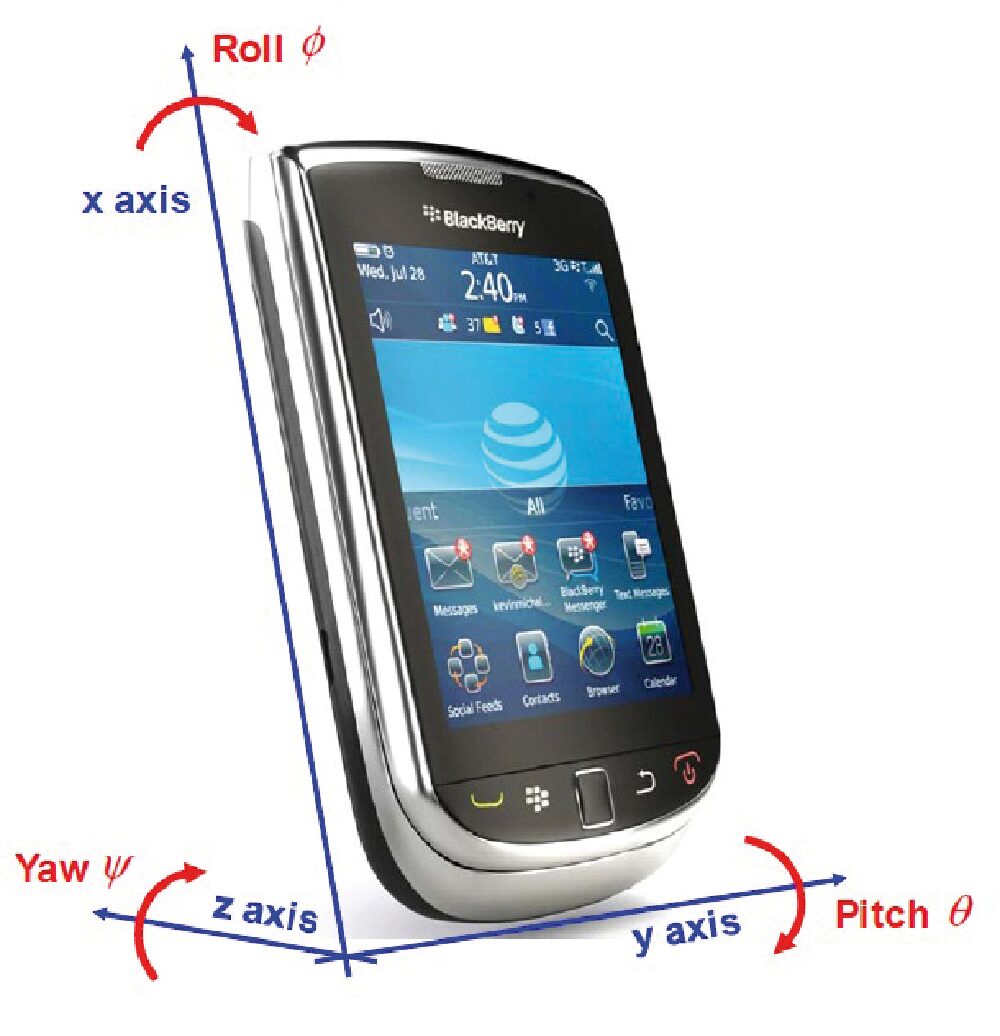
Fig. 17 Sistema di coordinate associato all’accelerometro e quindi all’apparecchio nel quale esso è integrato.
Un cambiamento dell’orientamento del dispositivo può essere descritto da una sequenza di rotazioni φ (roll), pitch (θ) e ψ (yaw) intorno rispettivamente agli assi x, y e z. L’accelerometro fornisce uscita +1g per qualunque asse orientato nella direzione dell’accelerazione di gravità. Quanto detto al punto 2) può essere espresso analiticamente dalla seguente relazione:
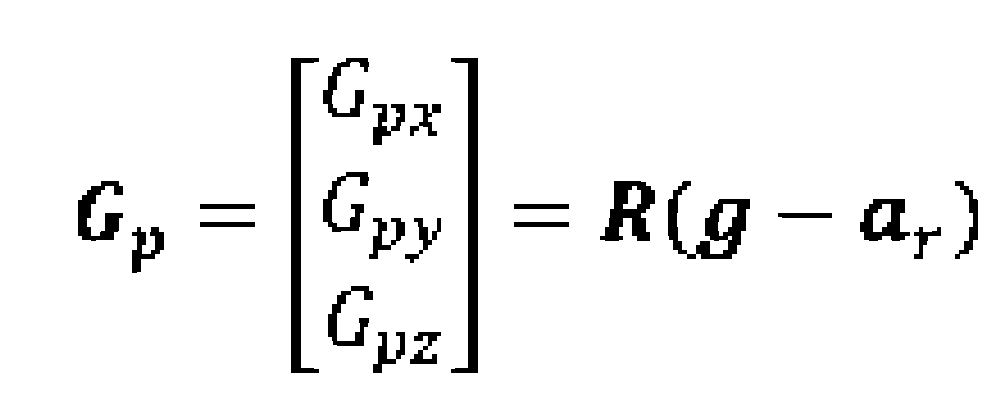
dove Gp è il vettore colonna avente come componenti le proiezioni del vettore g sui tre assi dell’accelerometro, R è la matrice di rotazione che esprime l’orientamento dello smartphone rispetto ad una posizione iniziale di riferimento, g ed a i due vettori di accelerazione (di gravità e lineare rispettivamente).
La precedente relazione è coerente con il fatto che se lo smartphone viene lasciato cadere (caduta libera) assumendo accelerazione lineare pari a g, ne consegue che Gp=0. Si suppone che l’accelerazione lineare sia nulla e che l’orientamento iniziale dello smartphone sia orizzontale, con l’asse z coincidente con la direzione del vettore accelerazione di gravità. La relazione precedente si riduce così a:
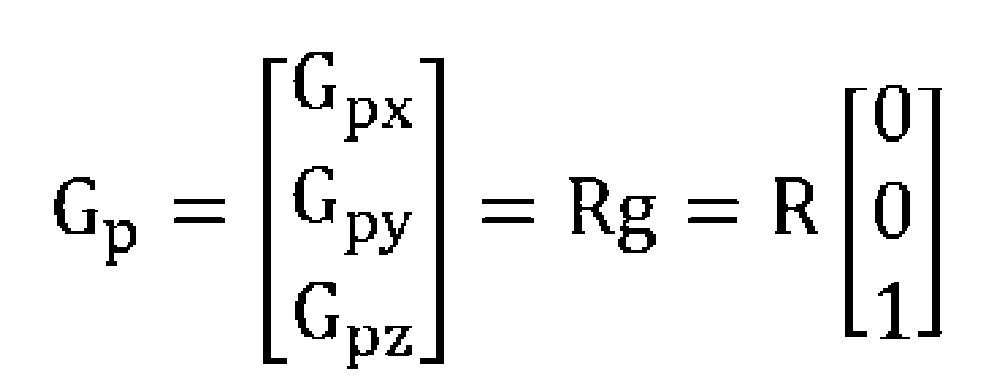
dove Gpx, Gpy e Gpz sono le tre componenti dell’uscita dell’accelerometro.
Nei precedenti paragrafi abbiamo introdotto la matrice di rotazione senza darne una definizione rigorosa. In due dimensioni (quindi nel piano), una rotazione è una trasformazione R(θ), che dipende da un angolo θ, e che trasforma il vettore (x; y) nel vettore:
x’ = x cos − y sin
y’ = x sin + y cos
È facile verificare, di conseguenza, applicando le regole del prodotto matriciale, che il nuovo vettore può essere espresso dal seguente prodotto:
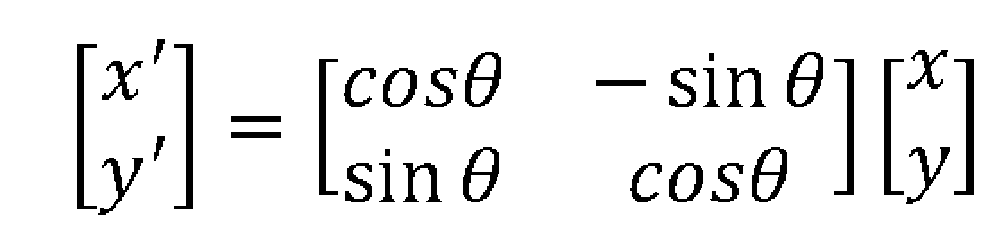
La matrice quadrata presente in questa espressione è chiamata “Matrice di rotazione” e descrive analiticamente la rotazione antioraria di angolo θ del vettore originario intorno all’origine.
Vi risparmiamo la trattazione matematica del caso, relativa all’evoluzione nello spazio piuttosto che nel piano, perché per complessità esula dagli scopi di questo articolo; chi vorrà approfondire la materia potrà trovare documentazione sul web NXP.
Nello spazio, esistono (si rimanda al suddetto riferimento) sei possibili combinazioni che portano a sei differenti risultati ognuno suscettibile di poter esprimere le componenti del vettore g dopo tre distinte rotazioni riferite ai singoli assi. In ciascuno di questi casi abbiamo una matrice di rotazione che può essere vista come il prodotto delle singole matrici di rotazioni ciascuna relativa ad uno dei tre assi.
L’accelerometro presenta tre uscite (le componenti del vettore g lungo i tre assi) ma esse sono vincolate sempre a dare come modulo del vettore 1g (supponendo presente la sola accelerazione di gravità). Comunque venga ruotato il sistema di riferimento solidale con l’accelerometro pertanto, note due componenti, la terza è definita automaticamente poiché il vettore accelerazione cadrà sempre sulla superficie di una sfera di raggio 1g. Il sistema gode cioè di due soli gradi di libertà. Ne consegue che gli ultimi quattro sistemi di equazioni non possono essere risolti in φ, θ e ψ mentre i primi due sì essendo le relative equazioni dipendenti da due soli angoli (roll e pitch).
In pratica, qualunque nuovo orientamento dal punto di vista della scomposizione di g lungo i nuovi assi di riferimento può ottenersi dalla sequenza di due sole rotazioni una di roll e l’altra di pitch. L’assenza della rotazione di yaw è fisicamente legata al fatto che il sistema dal punto di vista della scomposizione di g lungo le tre direzioni è insensibile a qualunque rotazione intorno a z. In altri termini se poniamo il nostro smartphone poggiato orizzontalmente sul tavolo e ne variamo l’orientamento lasciandolo però sempre orizzontale, il suo accelerometro non si accorge della variazione di assetto che stiamo apportando. Qualunque nuovo assetto diamo lasciando orizzontale l’apparecchio e ruotandolo intorno alla direzione di g, non viene avvertito.
L’orientamento dello smartphone, a partire dai tre valori ottenuti dall’accelerometro, può essere quindi ottenuto dalla risoluzione del primo sistema di equazioni o in alternativa del secondo eliminando la rotazione yaw e considerando due sole rotazioni roll e pitch.
Calcolo dell’inclinazione
Se l’accelerometro è in grado di restituire le componenti di g lungo i suoi tre assi, il prodotto scalare tra il vettore Gp avente queste componenti ed il versore dell’asse z (solidale con lo smartphone) fornisce la componente z dell’accelerazione di gravità (Fig. 18).
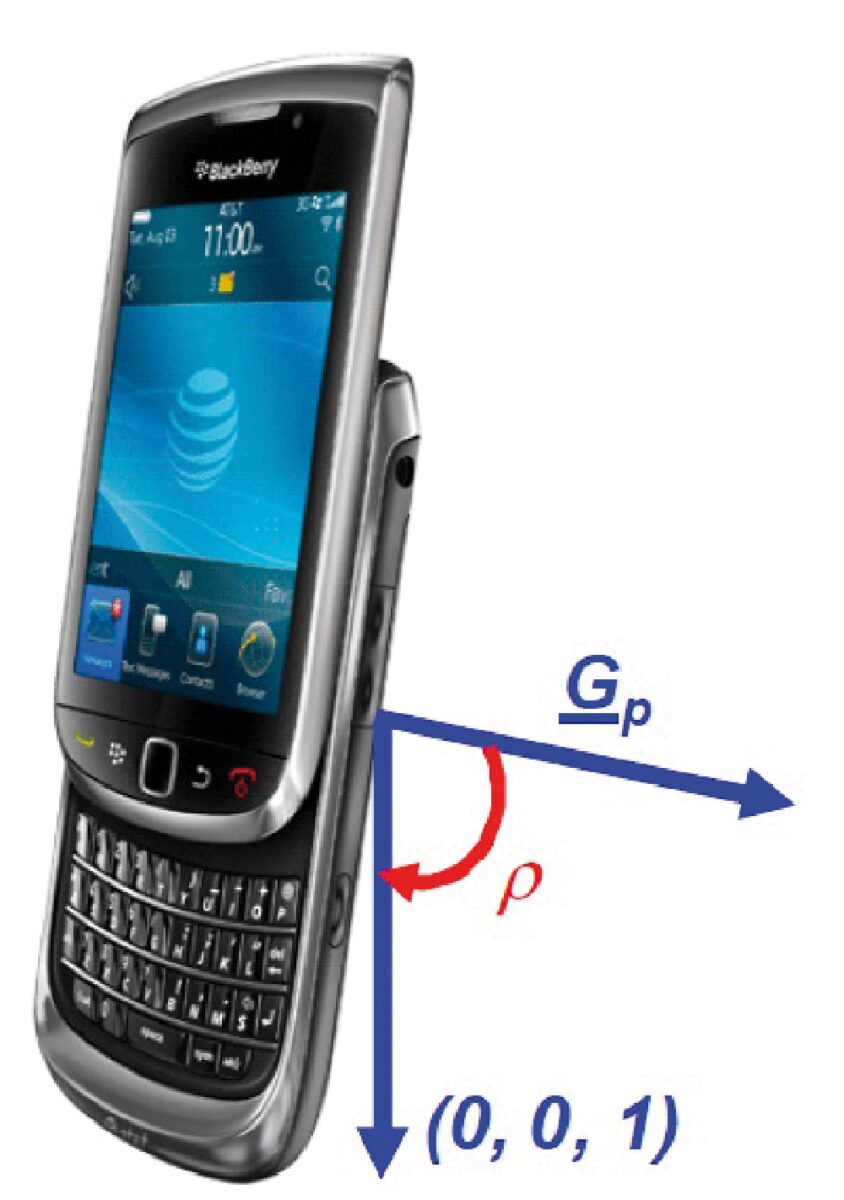
Fig. 18 Se l’accelerometro restituisce le componenti di g lungo i suoi tre assi, il prodotto scalare tra questo vettore (Gp) e il versore dell’asse z (solidale con lo smartphone) fornisce la componente z dell’accelerazione di gravità.
Senza scendere troppo nel dettaglio, diciamo che vale la relazione:
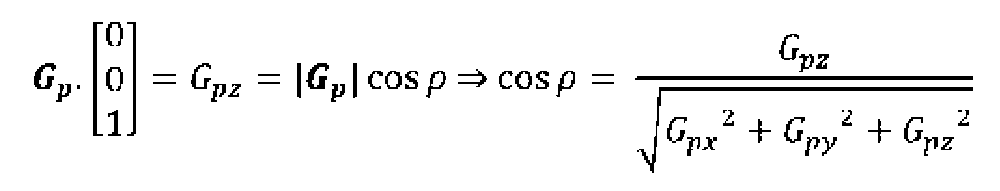
dalla quale è possibile calcolare l’angolo di inclinazione dell’asse z dell’accelerometro e quindi del dispositivo all’interno del quale lo stesso è montato rispetto alla verticale (vettore gravità).
Orientamento automatico
La prima applicazione su larga scala dell’accelerometro è stata la visualizzazione automatica dell’orientamento delle immagini sul display di smatphone e tablet. La Fig. 19 esemplifica il concetto. Sulla base di quanto esposto fino a questo momento, l’operazione può sembrare relativamente agevole da implementare grazie all’accelerometro. In realtà essa nasconde una complicazione.
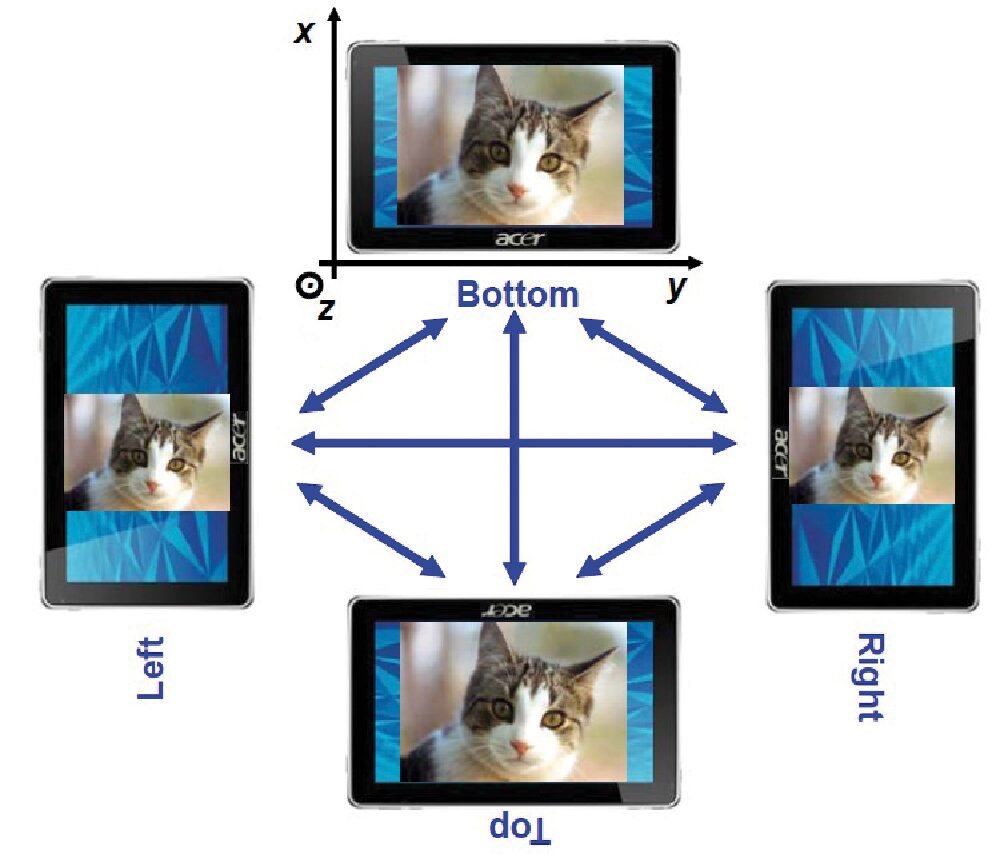
Fig. 19 Orientazione automatica (modalità portrait e landscape) delle immagini visualizzate sul display di un tablet.
Infatti, da qualunque delle quattro configurazioni di figura si parta è necessario che l’orientamento dell’immagine venga mantenuta quando si “corica” il tablet in maniera tale da disporlo orizzontalmente cioè con il display parallelo ad un tavolo che consideriamo come piano di appoggio. In questo stato infatti, qualunque dei quattro orientamenti dell’immagine, rispetto allo smartphone, sarebbe ugualmente valido dal punto di vista della scomposizione del vettore g (ma non dal punto di vista dell’utente!).
Evidentemente, per decidere correttamente l’orientamento dell’immagine quando si “corica” lo smartphone è necessario non solo riconoscere la posizione orizzontale ma avere anche informazione su quale sia lo stato da cui si proviene. È facile comprendere che una macchina a stati finiti basata sulle transizioni seguenti sia in grado di risolvere il problema:
(|Gpz|<0,5g)AND(|Gpx|>0,5g)AND(|Gpy|<0,4g) → cambia l’orientamento in TOP
(|Gpz|<0,5g)AND(|Gpx|<-0,5g)AND(|Gpy|<0,4g) → cambia l’orientamento in BOTTOM
(|Gpz|<0,5g)AND(|Gpy|>0,5g)AND(|Gpx|<0,4g) → cambia l’orientamento in RIGHT
(|Gpz|<0,5g)AND(|Gpy|<-0,5g)AND(|Gpx|<0,4g) → cambia l’orientamento in LEFT
Grazie alla sua implementazione, non solo la macchina è in grado di determinare correttamente la visualizzazione dell’immagine quando il display non è coricato, ma è anche in grado di lasciarla inalterata nel momento in cui, partendo da una di queste condizioni, lo si “corica”. Infatti, quest’ultima transizione porta alla condizione |Gpz|=1 per cui nessuna delle quattro condizioni precedenti è rispettata e l’orientamento dell’immagine rimane invariato.
Applicazioni basate sull’accelerometro
Oggi esistono numerose applicazioni per smartphone che sfruttano le potenzialità dell’accelerometro. Alcuni sono a tutti gli effetti dei giochi, altri hanno invece una reale utilità pratica. Ne citiamo alcune scaricabili gratuitamente e con le quali il lettore potrà condurre semplici e utili esperimenti.
Sensor Kinetics – È un’applicazione che consente di monitorare i sensori integrati nel proprio smartphone (di solito nel nostro smartphone sono integrati almeno un magnetometro e un sensore di prossimità oltre all’accelerometro). L’applicazione consente di monitorare le componenti x, y e z dell’accelerazione di gravità e di tracciarle in un grafico temporale (Fig. 20). Il secondo grafico riporta la misura dell’accelerazione mentre lo smartphone esegue la seguente evoluzione: verticale per circa tre secondi, coricato sul piano del tavolo per altri tre secondi, coricato di taglio sul lato lungo sinistro per ulteriori tre secondi. Si deduce facilmente che l’asse y coincide con la direzione in lunghezza del dispositivo, l’asse z con la perpendicolare al piano del display mentre il terzo asse coincide con il lato corto del dispositivo. Il terzo grafico temporale mostra un’evoluzione simile a meno dell’ultima variazione di posizione che porta il dispositivo a essere posizionato verticalmente ma a testa in giù da cui l’accelerazione negativa misurata lungo l’asse y.
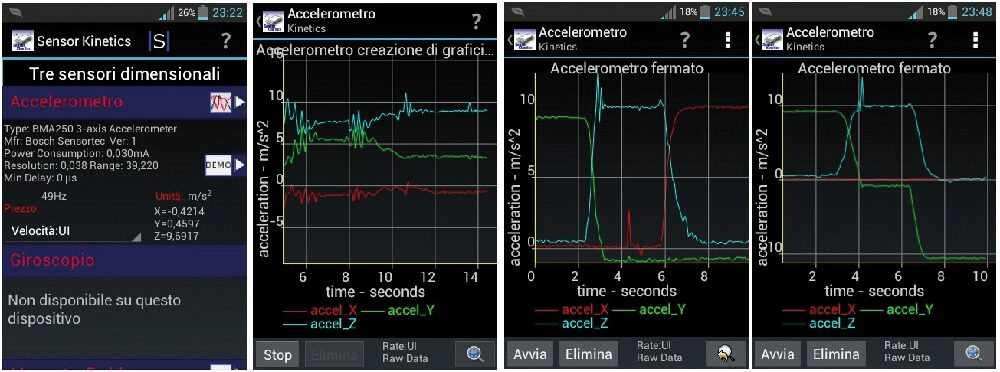
Fig. 20 A sinistra, la schermata principale di Semnsor Kinetics e a destra il tracciamento temporale delle componenti dell’accelerazione di gravità.
Livella – La livella (Fig. 21) è un’applicazione insensibile alle rotazioni intorno ad un asse parallelo all’accelerazione di gravità, che consente di misurare l’inclinazione del display rispetto a un piano orizzontale. Si tratta in pratica dell’inclinometro trattato nei precedenti paragrafi.
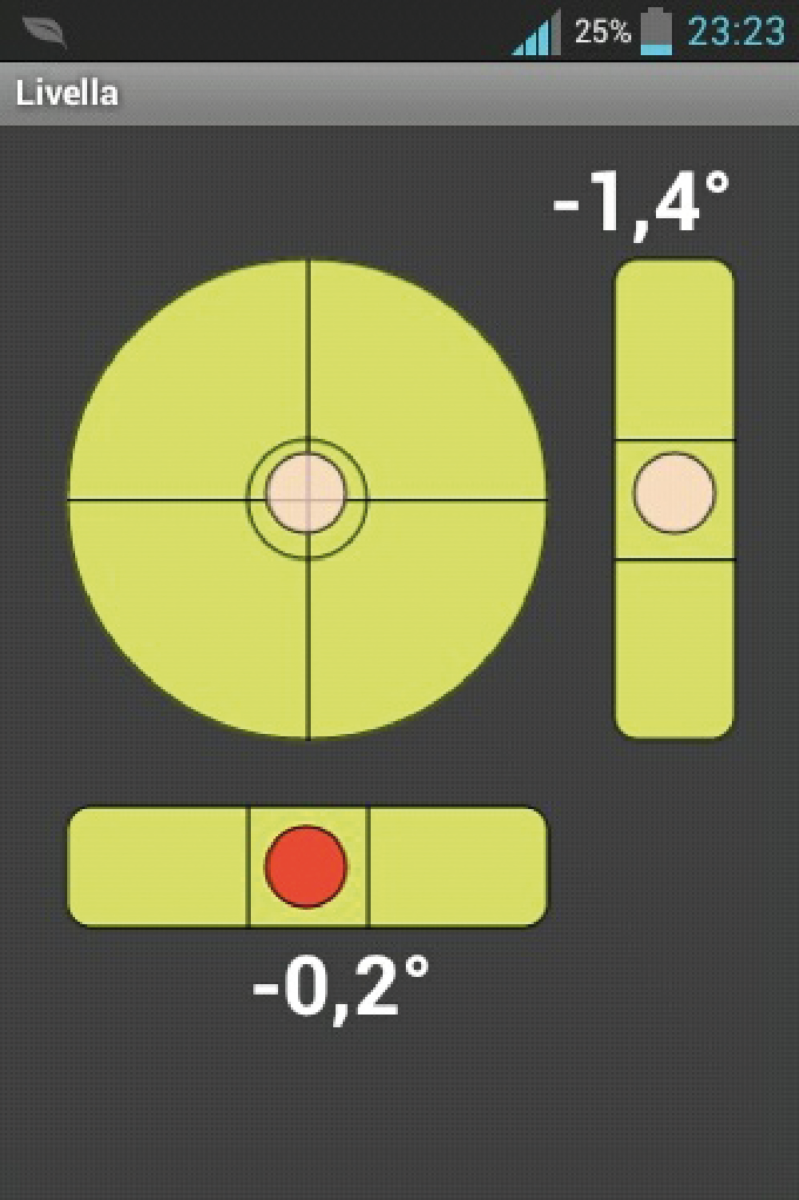
Fig. 21 Livella elettronica implementata come applicazione Android per smartphone.
Contapassi – Attraverso l’accelerometro è possibile rilevare la regolarità con cui si susseguono i nostri passi quando portiamo con noi il nostro smartphone. Di conseguenza è possibile realizzare delle applicazioni che sentendo tale regolarità sono in grado di fungere da contapassi elettronico (Fig. 22).
Misuratore di distanze – Sfruttando la trigonometria si può usare l’accelerometro per misurare una distanza. Fissata l’altezza cui si tiene lo smartphone, si punta la fotocamera in esso integrata al suolo nel punto di cui si intende calcolare la distanza. L’apparecchio misura l’inclinazione del dispositivo. Questa informazione, unitamente all’altezza alla quale teniamo il dispositivo (dato che inseriamo come taratura), consente di ricavare l’informazione desiderata con semplici calcoli trigonometrici. Si potrebbero citare altre applicazioni simili che consentono il controllo del dispositivo tramite “gesture”, che per esempio cancellano lo schermo quando si agita lo smartphone o che ne bloccano la sveglia quando lo capovolgiamo. Lasciamo al lettore il compito di arricchire la lista.
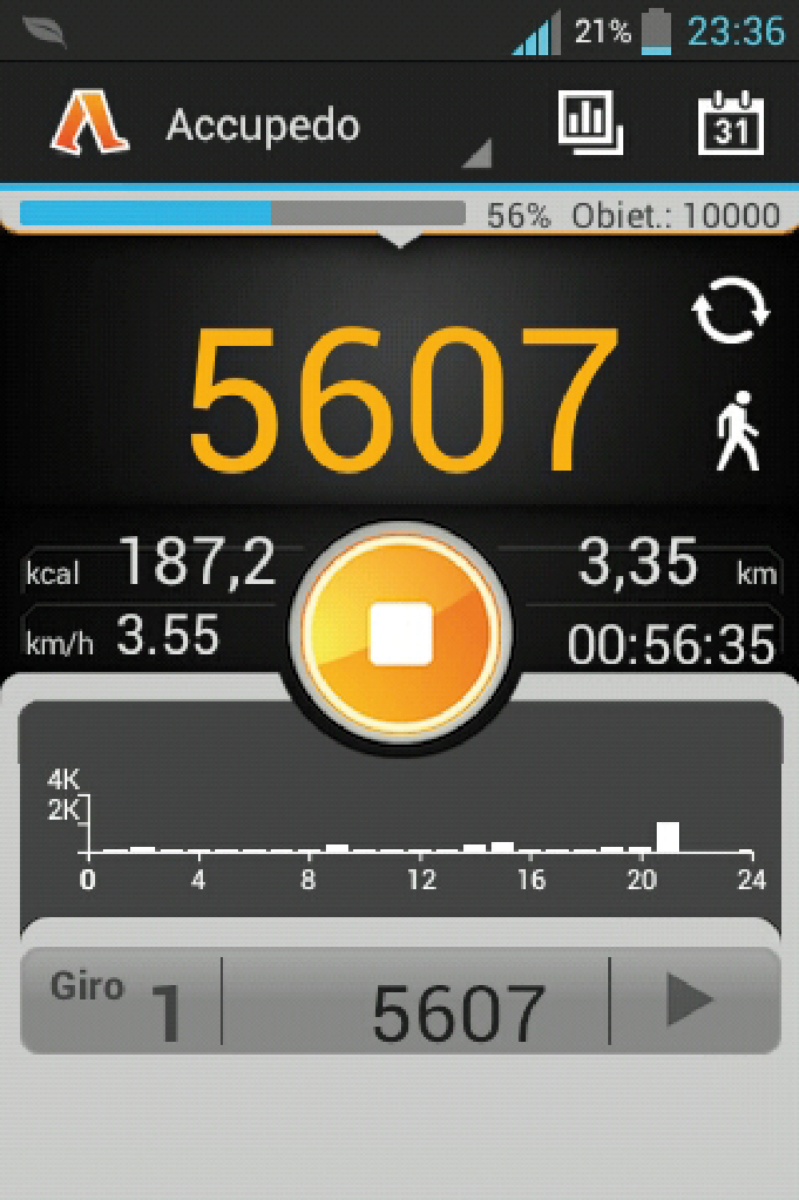
Fig. 22 Accuped, applicazione Contapassi elettronico o per smartphone.
Conclusioni
Gli accelerometri, i MEMS in particolare, sono entrati a far parte della nostra vita quotidiana; la possibilità di rilevare una rotazione, di fare da inclinometro, di rilevare l’accelerazione di parti meccaniche in movimento (si pensi alla misura dell’accelerazione laterale nei veicoli, allo scopo di controllare le sbandate e attivare l’azionamento automatico del sistema di frenatura) rendono questi sensori utili in un’infinità di applicazioni. La misura dell’accelerazione di bracci mobili, per esempio, risulta fondamentale in molte applicazioni della robotica e dell’automazione.
Diversi modelli di accelerometri utilizzati sugli smartphone possono registrare fenomeni sismici perché capaci di garantire prestazioni prossime a quelle degli accelerometri professionali; in quest’ottica, alcuni centri di ricerca in ambito sismologico hanno intravisto la possibilità di creare reti di rilevamento sismico basati sugli accelerometri contenuti in apparecchiature portatili come smartphone e computer di utenti civili.




3 Commenti